Tree ?
* 여태는 다 Linear list ; 선형적으로 연결된 데이터에 유용 ! serially ordered data
tree는 -> 계층구조 데이터 저장에 유용 ! hierarchically ordered data
= 자료와 그 다음 자료의 위치 정보가 저장된 비선형의 자료구조
> 트리 성질
- 루트 노드 제외하고 모두 하나의 부모 노드를 가진다
- 여러개의 자식 노드를 가질 수 있다
- 한 노드에서 다른 노드로 가기 위한 경로가 유일하다 ! (-> 트리의 조건 !)
> 쓰이는 곳
- file system
- compiler
- graphics
- database (index)
> 기본 용어
• root : top of the hierarchy
• leaf / terminal node : 맨 끝 노드
• siblings : 형제 노드. 부모가 같을 때 (같은 층애들)
• children : 해당 노드 아래 노드
• grandchildren : 그거의 아래노드 (한번더 -> great grandchildren)
• node : 점
• branch : 이은 선 ( = link ! )
• subtree

• degree = 한 노드에 연결된 자식 노드의 수
-> degree of tree = 노드 중 최대 degree를 트리의 디그리로 봄
• level : 루트를 레벨 1로 보고 점점 커진다
-> height/depth = maximum level !
tree 표현하는 방법
1. left child-right sibling representation
-> 왼쪽 자식 노드랑 같은 레벨의 sibling 정보를 담는다

2. representation as a degree-two tree
-> left, right child를 가지는 tree ! 내가 아는 일반적인 트리 형식
Binary tree
: 자식노드가 최대 두 개인 노드들로 구성된 트리 ! (무조건 가져야 하는 것은 아님. 1개일 수도 잇음 !)
struct Tree_Node{
ElementType data;
Tree_Node* Left;
Tree_Node* right;
}
성질
• level i의 최대 노드 개수는 2^(i-1) (루트레벨이 1이라고 봣을 때)
• depth k일때 전체 노드 최대 개수는 2^k -1 (시그마 사용^^)
• 리프노드의 개수가 n0이고, degree 2인(자식2개인) 노드의 개수가 n2일 때, n0=n2+1 !!
-> 증명 ; branch와 branch=node+1 이용!

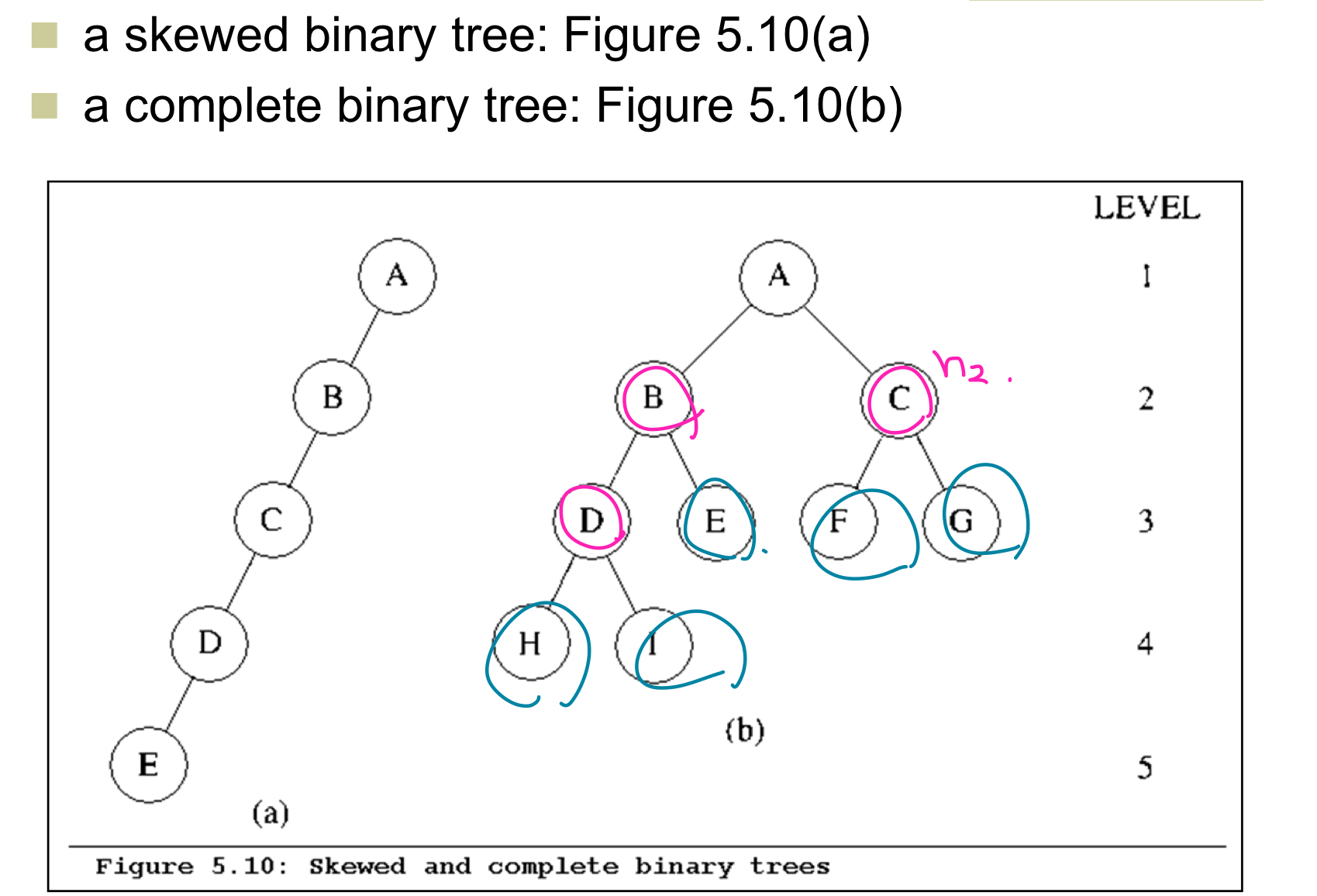
full binary tree (걍꽉참)
: 리프노드 제외 모든 노드의 자식노드가 2개
-> depth가 k일때 2^k -1 개의 노드를 가진다
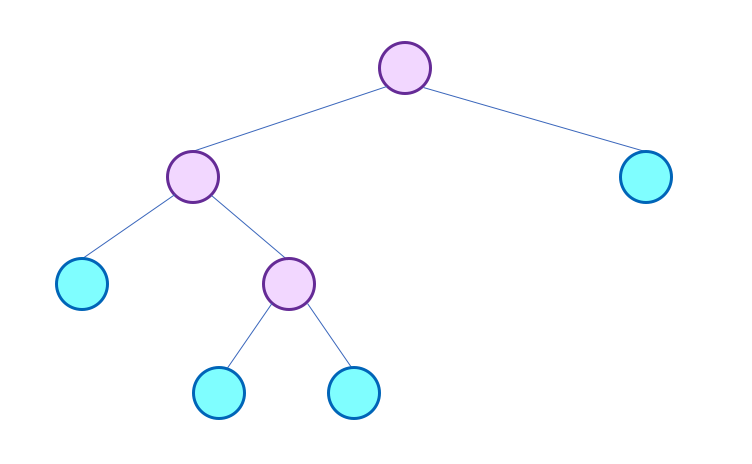
complete binary tree (뭔가 더 complete. 순서대로 왼쪽부터 차는거)
마지막 level 을 제외한 나머지 level 에 node 들이 가득 차있고,
마지막 level 에서 node 는 가장 왼쪽 부터 채워지는 형태
* perfect b tree = 진짜 다차있는거 ^.^
구현 representation

1. Array representation
위에 사진에서 해당 숫자를 인덱스로한 배열을 만든 후 그 배열안에 문자 넣는다 ! (존재하는 것들에 대해)
-> 메모리 낭비 ! 노드 추가/삭제를 위해서는 memory 옮기기를 해야하는데 이건 최악의 연산 ! 오엠쥐
- skewed tree -> wasteful !!
- 중간에 잇는 애 삭제, 추가하면 memory movement !! 오엠쥥
2. Linked representation
struct{
int data;
pointer left;
pointer right;
}활용
A. Binary search tree
- 바이너리 트리 ; left에 작은 값들, right에 같거나 큰 애들 저장함 !!
• 알고리즘
1. Ascend()
-> inorder traversal을 한다 !
- 복잡도 : O(n) (모든 원소 다하니까 ! )
2. Search()
- 복잡도 : O(log n) (레벨이 log n 이니까)
3. Insert()
-> 자리 찾아서 삽입함 ! -> 무조건 리프에 들어감!
- 복잡도 : O(height) = O(log n)
a. 노드 존재 하는지
b. 해당 노드보다 데이터 작으면 왼쪽자식으로
c. 해당 노드보다 크면 오른쪽 자식으로
-> 이걸 반복해서 들어갈 자리 찾음 !
4 Delete()
-> 네가지 경우 !
♡ key에 해당하는 노드 없음
♡ 리프노드에 잇음-> 걍삭제
♡ degree1인 노드임 -> 자식 노드를 끼워주면됨 ^^ 왼/오중 잇는거로 !
♡ 디그리 2임 ! 자식 두개잇음 -> 오른쪽 노드중 가장 작은걸로 바꾸거나 왼쪽 자식 노드들중 가장 큰거로 바꿔줌
-> 가장 큰 노드는 리프노드거나 degree 1인 노드임 ! 이 연산은 아주쉬움 위에서 봣던것처럼 ! 그래서 이렇게 해준당
• 코드
Search
- recursive
-> 같/작/큰
element* search (treePointer root, int key){
if (!root) return NULL;
if (k==root->data.key) return &(root->data);
//작으면 왼쪽으로 재귀
if (k<root->data.key) return search(root->leftChild, k);
//크면 오른쪽으로 재귀
return search(root->rightChild,k);
}- iterative (재귀 사용 x) ; 같.작.큰
element* iterSearch(treePointer tree, int k){
while(tree){ // tree = 노드. 노드가 존재할 때 까지 하는겅 없으면 알아서 null 반환 ^^
if (k==tree->data.key) return &(tree->data);
if (k<tree->data.key) tree = tree->leftChild;
else tree=tree->rightChild;
}
return NULL;
}
Insert

* 먼저 넣을 노드를 안찾고 그냥
노드를 malloc해서 할당한 후
재귀로 insert(tmp->leftChild) / insert(tmp->rightChild) 하면 됨
이렇게 해줘도 된다 !
a. 노드 존재 하는지
b. 해당 노드보다 데이터 작으면 왼쪽자식으로
c. 해당 노드보다 크면 오른쪽 자식으로
-> 이걸 반복해서 들어갈 자리 찾음 !
// 재귀사용 !!
void insert(Node** p, int value){
//노드 없으면 여기 집어넣음 (재귀의 마지막엔 여기에 들어감)
if((*p)==NULL){
* p=malloc하고 value넣음 //안에다 넣어줘야함 재귀할때마다 뉴 노드 만들 순 없으니 ㅋ
left,right=NULL;
} //노드 이제 존재할때 -> 들어갈 곳 찾는다
else if((*p)->data > value){
insert(&(*p->left), value);
}else{
insert(&(*p->right), value);
}
}* 쉬운데 주의점 !!
- NULL일때 *p에 malloc해줘야한다 !! 값들도 *p->value 이렇게 넣어야함 !! 이중포인터라서 !!
- 재귀할때 left, right넣을때 이건 이중포인터이기때문에 &((*p)->leftChild) 꼭 이렇게 넣어줘야함 !!!중요
• joining and splitting binary tree

- twowayjoin: 두 서브트리합치는데, 이때 루트는 큰트리중 젤 작은 노드 또는 작은트리중 젤 큰 노드가 되고 그 노드, big, small을 합치는 threewayjoin이 된다!
B. Expression Tree
; expression을 표현한다 (식)
(a*b)+c 이런거. 뒤에서 계속 할 것
Binary tree traversal (트리 순회)
-> 모든 노드를 한번 방문한다
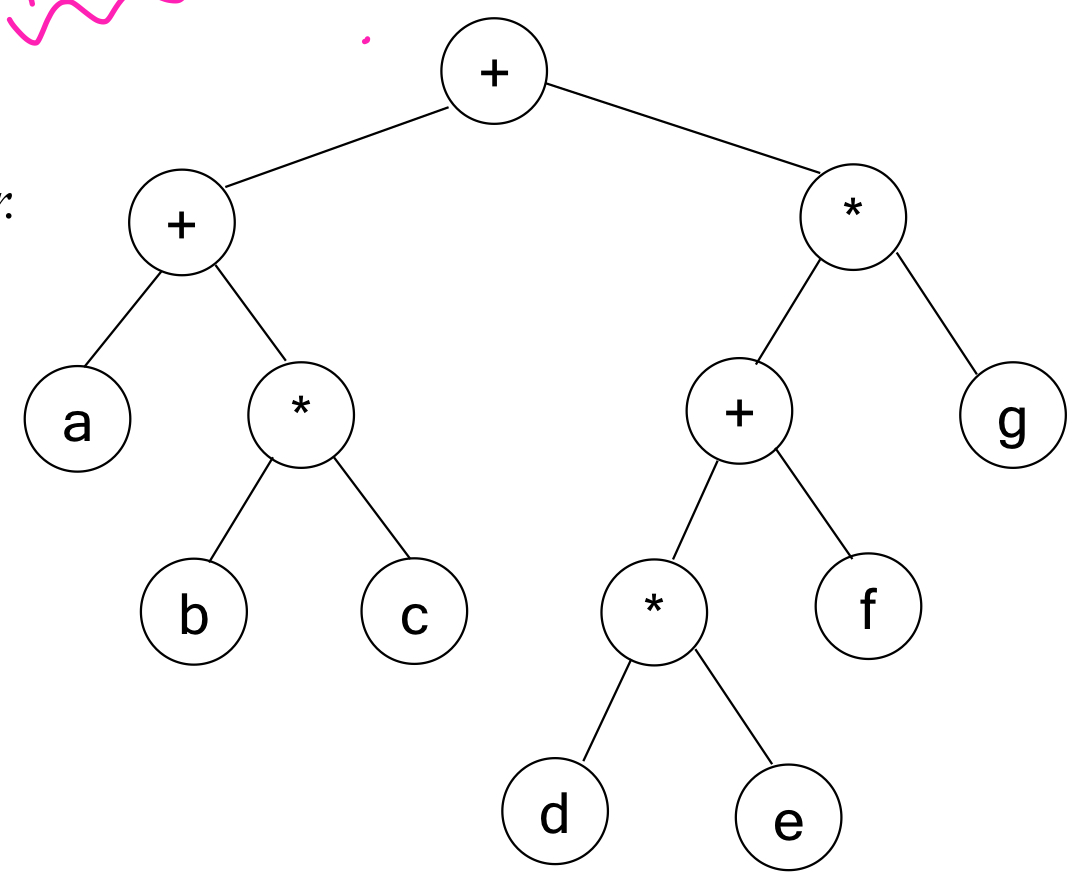
1. inorder ; LVR (평범) ; infix 식
-> a+b*c+d*e+f*g
= 연산자 그냥 그대로. 평범한 식!
2. postrorder ; LRV (넘빨리해서 가운데가 뒤로 밀린 것) ; postfix 식
-> abc*+de*f+g*+
= 연산자 괄호 뒤로 다 한거
3. preorder ; VLR (가운데가 넘 예쁜 것) ; prefix 식
-> ++a*bc*+*defg
= 연산자 괄호 앞으로 다 한거
코드
a. Inorder
- recursive
: 왼쪽 다 검사 -> 가운데 프린트 -> 오른쪽 다 검사
void inorder (treePointer ptr){
if(ptf=NULL){
return;
} // 실습코드는 이렇게되어잇다 ~~
inorder(ptr->leftChild);
printf("%d", ptr->data);
inorder(ptr->rightChild);
}if NULL -> return 꼭 하기 !!!!
- iterative ; 재귀 x ! -> 스택 이용 !!
: stack에 왼쪽자식 노드 계속 넣고 가운데노드 프린트하고 오른쪽노드를 똑같이 탐색시작한다 !
(오른쪽노드의 왼쪽노드계속 넣는거 반복)
stack이 비면 탈출 !
전체는 while문
1. 왼쪽 노드들을 스택에 다 담는다
2. 하나 pop한다 - 이게 null이면 break;
3. 해당 노드 프린트
4. 오른쪽 노드로 이동
void iterInorder(tree Pointer node){
treePointer stack[MAX_STACK_SIZE];
for(;;){ // = while !
//왼쪽 노드들을 쭉 담는다
for(;node;node=node->leftChild){// ;node;조건은 node가 null이 아닐때까지 !!
push(node); //스택에 담는당
node = pop(); //하나빼낸다
if (!node)
break; // 노드가 없다 = 스택에 암것도 안들어있다 -> 끝 ~~
//가운데꺼 출력 후 오른쪽 노드 탐색을 시작한당 (없으면 그냥 아무것도안담고 하겟지요 ~ )
printf("%d", node->data);
node=node->rightChild;
}
}
b. preorder
: 가운데 -> 왼 -> 오
printf("%d", ptr->data);
preorder(ptr->leftChild);
preorder(ptr->rightChild);
c. postorder
: 왼->오->가운데
postorder(ptr->leftChild);
postorder(ptr->rightChild);
printf("%d", ptr->data);
+) level order traversal
: 같은 노드인 애들 레벨 1부터 쭈루룩 프린트하는 것 -> queue 사용 !
-> 해당 노드를 프린트하고 왼, 오 노드를 큐에 담음
-> 그리고 큐를 차례로 읽음
읽을 때 각자의 왼, 오 노드를 큐에 담음 !!
void levelOrder(treePointer ptr){
treePointer queue[max_size];
if (!ptr) return; //암것도 없으면 걍 끝 ~
addq(ptr); //큐에 첫 노드 담는다
for(;;){ //큐가 텅 빌때까지 돈다
ptr=deleteq(); //담은 노드 나옴
if(ptr){ //큐가 존재하면 한다
printf(ptr->data);
if (ptr->leftChild) addq(ptr->leftChild);
if (ptr->rightChild) addq(ptr->rightChild);
}
}
}
* stack 없이 traversal 하는 법 ?
1. 각 노드에 parent field를 추가한다 !! trace back 할 수 있도록
2. b tree를 threaded binary tree로 나타낸다 ~~
-> root로 돌아갈 수 잇다 ~~ (뒤에 나옴)
Additional Binary Tree Operations
Copying binary trees
: binary tree 복사하는 것 -> postorder 알고리즘 수정해서 함 !
treePointer copy(treePointer original){
treePointer temp
if (original){ // 존재하면
temp에 malloc하기
temp->leftChild=copy(original->leftChild);
temp->rightChild=copy(original->rightChild);
temp->data=original->data;
return temp;
}
return NULL;
}temp 할당 !!
return temp !!
Testing equality
: 두 바이너리 트리가 같은지 확인한다 ~~

return (둘다 안존재) || ( first존재 && second 존재 & data같음 && equal(left트리들)&& equal(right트리들) )
( equal = 재귀 !! 리턴 !! )
Satisfiability problem
^은 and, v는 or인 듯 !
이걸 tree로 나타내고 postorder을 취해서 1이 되는지 아닌지를 확인할 수 있음!

Threaded binary trees
: 트리의 깊이가 증가하는 만큼 효율성이 저하되는 것을 방지하기 위함
노드의 link가 비어잇다 ! (자식노드가 없다) -> 다른노드 연결한다 !! 포인팅 해준다 !!
- LeftChild 가 NULL -> inorder predecessor 로 대체 ! (이전꺼)
- RightChild가 NULL -> inorder successor 로 대체 ! (다음꺼)
* 맨 양 끝 노드 -> root node에 연결해준다
• 자료구조 ; linkfield (left/right child) 만 있으면 안됨. 왜냐면 이게 만들어준 링크인지 원래 이어져잇던 자식인지 모르기 때문에
-> 2개의 flag field 가 필요 !
leftThread = 이전꺼. 선행자
rightThread = 다음꺼. successor !(연속자?)

leftThread, rightThread 가 true 이면 쓰레드라는 뜻 ! (thread 인지 아닌지를 알려줌)

inorder predecessor, successor 찾는법
- inorder successor : 자신(x)의 오른쪽 subtree중 가장 왼쪽의 노드
( 그 노드의 leftThread = true 이고 그 노드의 왼쪽링크는 x일거임. 오른쪽노드에서 계속 왼쪽으로 이동하여 leftThread가 true인 애 찾으면 됨. 그리고 해당 노드 반환하면 됨)
- inorder predecessor : 자신의 왼쪽 subtree중 가장 오른쪽에 있는 노드
(왼쪽 노드로 한번 이동 후 계속 오른쪽으로 가서 rightThread 있는 애 찾아서 반환)
-> 코드
successor 찾기
threadedPointer insucc (threadedPointer tree){
threadedPointer temp;
temp=tree->rightChild; //오른쪽 서브트리중에서 찾아야하므로 일단 오른쪽 자식으로 이동
if(!tree->rightThread){ // 오른쪽 노드가 있을 경우 (없을수도잇으니가 ㅋ)
while(!temp->leftThread) // temp에 leftThread가 있으면 루프나옴 !!
temp=temp->leftChild
}
return temp;
}predecessor은 left, right만 바꿔주면 됨
inorder traversal 코드
-> insucc 이용 ! (다음 노드 찾는 코드)
짱쉬움! 루프에서
다음노드찾음 -> 없으면 끝 , 있으면 출력
void tinorder (threadedPointer tree){
threadedPointer temp = tree;
for(;;){
temp=insucc(temp); //다음 노드 찾음
if(temp==tree) break; //다음 노드 없으면 루프 나감
printf(temp->data); //출력 ^^
}
}
threaded b tree에 node 삽입하기 !
-> rightChild에 붙이기
1. 오른쪽 자식이 없으면 단순히 삽입 !
2. 오른쪽 subtree 존재하면 그 노드 삽입 후 그 노드의 subtree로 만든다
* 그 어느경우에도 삽입하는 그 노드의 왼쪽 자식은 생기지 않는다 ! -> 꼭 precessor 찾아줘야함!
쉬워요
s노드의 오른쪽자식에 r삽입하기 !
일단 함수의 parameter = 포인터형 ^,^
-> r의 오/왼 -> s의 오 -> r 선행자 처리
1. 오른쪽 자식 그대로 대입
r->rightChild=s->rightChild; //그대로 노드 연결~
r->rightThread=s->rightThread; //이 값도 넣어주깅
2. 왼쪽 pre 대입 (=parent)
r->leftChild=parent; //얘는 무조건 왼쪽자식이 없어서 이값은 predessesor이므로 무조건 parent.
r->leftThread = TRUE;
3. s의 오른쪽 자식 쟤로 바꿔줌
s->rightChild=r; //r먼저 바꿔주고 이거해야댐!!왜냐면 r바꿀때 이정보 필요하니까
s->rightThread=FALSE; //무조건! 당연
4. r에 오른쪽 자식들이 있으면 그 자식중에는 r이 선행자인 애 무조건 존재 ! -> 그거 찾아줌
if(!r->rightThread){ // 자식이 있으면
temp=insucc(r);
temp.leftChild=r;
}
!! 다 두줄 !!
s에 r 삽입
!! 자식이잇으면선행자처리!! (!r->rightThread) = 자식이 잇다. thread가 false여야 자식이 있는 것!
(다음꺼가 얘를 pre로 가진다)
'2-1 > 자료구조 (c)' 카테고리의 다른 글
| Heap (0) | 2022.05.30 |
|---|---|
| Stack, queue (0) | 2022.04.17 |
| Skip List (0) | 2022.04.11 |
| List (0) | 2022.04.11 |
| 1. about C (0) | 2022.04.04 |