Concepts ; Heap 이란
정의 : 여러개의 값들 중에서 가장 큰 값 / 가장 작은 값을 빠르게 탐색하도록 만들어진 binary tree 자료구조
• complete binary tree (완전 이진 트리) 임 ; 맨 아래 레벨 빼고 다 채워져있고, 맨 아래 레벨애들은 왼쪽부터 채워저 있는 것
-> 높이가 h일때 총 노드 개수는 2^h ~ 2^(h+1) -1 가 존재한당 (h-1 높이에서는 2^(h-1) -1 )
( full : 자식이 0개 또는 2개인 것 )
• 부모노드의 키가 자식보다 같거나 크다 (MAX heap) - root 가 젤 큼
( MIN heap은 자식이 더 크겠지용 )

기능
• push
: 해당 값을 완전 이진트리가 되도록 젤 왼쪽 자식 노드에 넣는다
그리고 부모값과 비교해서 계속 바꿔가다가 부모가 더 크거나 같으면 끝~
• pop
: 루트를 리턴한다 (arr[1])
그리고 자식중 젤 오른쪽에 있는 애를 루트로 데려온다 (완전 이진 트리 만족하기 위함)
자식이 더 크면(둘중암거나) 더 큰애!!랑 바꿔준다 이거 반복
Priority Queue (우선순위 큐)
* 큐 = first in first out. (high priority 가진애(=먼저 들어간 애)가 먼저 나온다)
(우선순위가 높다=더앞에 있다. 더 먼저나온다)
우선순위 큐 = 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 자료구조 , 먼저 처리 되는 것 (delete. pop)
힙으로 구현가능! heap-based
(여기선 우선순위가 크다 = 숫자가 더 크다!)
맥스 힙 구조 = 우선순위가 높은(숫자 큰)애를 부모에 위치함 -> pop하면 우선순위 젤 높은 루트에 있는 애가 나옴
그래서 우선순위 큐는 힙으로 구현되는 것!
-> O(log n)의 복잡도를 갖게 됨 !
* 다른 자료구조를 사용하면
- unordered linear list
맨 뒤 삽입: O(1) (그냥 넣기만 하면되니까) / 가장큰키 가진애 삭제: O(n) (모두 탐색해야됨)
- ordered linear list
삽입: O(n) (다 탐색해서 넣어야 하므로) / 삭제 : O(1) (맨뒤에 있는거 삭제하면 되니까)
복잡도 : O(n log n) !!
Selection tree - Winner tree

- 트리 초기화
• 이걸 이용한 정렬
: 승자 = 젤 작은 값. 이걸 순서대로 리턴함
그리고 그 루트 노드는 트리에서 제거함
이걸 n번 반복하면 정렬된 숫자 배열을 얻을 수 ㅇ
- 복잡도:
트리 초기화 O(n), 승자 찾는 과정 O(log n) (=트리의 height) 이 승자찾기를 n번 -> O(nlogn)
=> O(n*log n) !
위너삭제하고replay : O(log n) , remove/replace 위너 and replay: O(log n)
위너 get : O(1)

이런식으로 1 삭제^^ (루트 삭제^^)
Loser tree
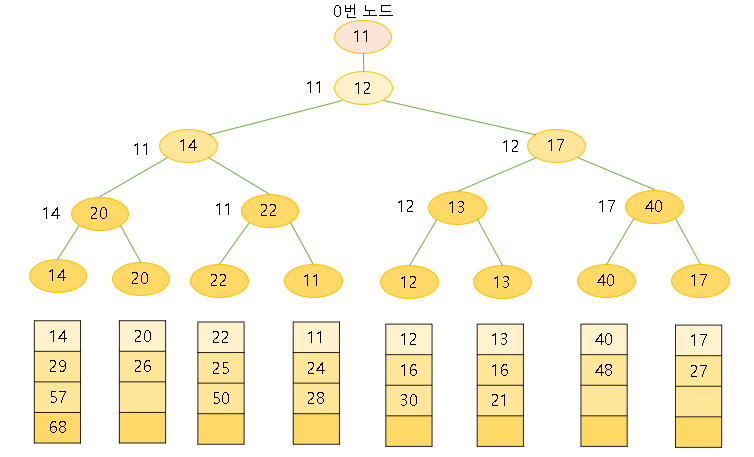
이기는애 = 더 작은애
패자(더큰애)를 부모에 기록하고
승자를 대결시켜 그 부모에 기록함

굳굳
total 초기화 복잡도
-> O(n)
replay 복잡도 (요소 하나 바뀔 때)
-> O(log n)
'2-1 > 자료구조 (c)' 카테고리의 다른 글
| Hash (0) | 2022.05.31 |
|---|---|
| AVL tree (0) | 2022.05.30 |
| Stack, queue (0) | 2022.04.17 |
| Binary tree (0) | 2022.04.13 |
| Skip List (0) | 2022.04.11 |
